一、适用课程
数据分析方法与R语言应用、卫生统计学、医学统计学
二、教学目标
(1)理解主成分分析的来源和应用场景;
(2)理解主成分分析的定义;
(3)掌握运用R语言求解多变量主成分的方法;
(4)学会结合研究问题解释求得的主成分。
三、案例资料
305例研究对象的八项身体测量指标数据,八项指标分别为height(身高)、arm.span(臂展)、forearm(小臂长)、lower.leg(小腿长)、weight(体重)、bitro(股骨转子间径)、chest.girth(胸围)和chest.width(胸宽)。相关系数矩阵如下:
| |
height |
arm.span |
forearm |
lower.leg |
weight |
bitro |
chest.girth |
chest.width |
height |
1 |
0.846 |
0.805 |
0.859 |
0.473 |
0.398 |
0.301 |
0.382 |
arm.span |
0.846 |
1 |
0.881 |
0.826 |
0.376 |
0.326 |
0.277 |
0.415 |
forearm |
0.805 |
0.881 |
1 |
0.801 |
0.38 |
0.319 |
0.237 |
0.345 |
lower.leg |
0.859 |
0.826 |
0.801 |
1 |
0.436 |
0.329 |
0.327 |
0.365 |
weight |
0.473 |
0.376 |
0.38 |
0.436 |
1 |
0.762 |
0.73 |
0.629 |
bitro |
0.398 |
0.326 |
0.319 |
0.329 |
0.762 |
1 |
0.583 |
0.577 |
chest.girth |
0.301 |
0.277 |
0.237 |
0.327 |
0.73 |
0.583 |
1 |
0.539 |
chest.width |
0.382 |
0.415 |
0.345 |
0.365 |
0.629 |
0.577 |
0.539 |
1 |
三、课前准备
(1)下载安装R软件;
(2)回顾变量之间相关系数的概念,复习矩阵的基本运算和矩阵的特征值和特征向量的概念;
(3)预习《R语言医学数据分析实战》中第12章第一节内容。
四、内容安排
(一)主成分分析的由来和应用场景(5分钟)
在医学研究与实践中,往往需要测量研究对象的很多个指标,收集大量的数据以便分析和寻找规律。多指标大样本无疑会为研究和应用提供丰富的信息,但也在一定程度上增加了数据收集的工作量。更重要的是,在多数情况下,许多指标之间可能存在相关性,从而增加了问题分析的复杂性。
例如,为了评价儿童的生长发育情况,研究者收集了一批儿童的身高、体重、胸围等八个指标的资料。如何利用这八个指标对研究对象做出评价呢?如果仅用其中一个指标作评价,会损失很多有用的信息,容易产生片面的结论。如果分别用每一个指标作评价,那么这种评价是孤立的,而不是综合的,所得结论可能相互矛盾。我们需要找到一种合理的方法,既能减少分析指标,又能尽量少损失原来指标所包含的信息。
本节要讨论的主成分分析(Principal Component Analysis,PCA)是在确保数据信息损失最小的原则下,把多个指标转化为少数几个不相关的综合指标的数据降维方法。主成分分析是由Hotelling于1933年首先提出的,其本质就是“降维”,即将高维数据有效地转化为低维数据来处理,解释变量之间的内在联系,进而分析解决实际问题。
(二)主成分分析的定义(10分钟)
主成分分析实际上是对原始变量进行线性变换,主成分就是原始变量的线性组合。假设有m个原始变量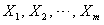 ,我们想找到这些变量的m个线性组合
,我们想找到这些变量的m个线性组合
 ,即
,即
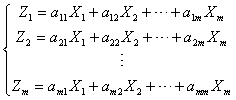 ,
,
其中, 互不相关,且Z1的方差最大,称之为第一主成分,Z2的方差次之,称之为第二主成分,余类推。此外,各线性组合的组合系数均为单位向量,即
互不相关,且Z1的方差最大,称之为第一主成分,Z2的方差次之,称之为第二主成分,余类推。此外,各线性组合的组合系数均为单位向量,即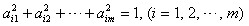 。上式的矩阵形式为:
。上式的矩阵形式为: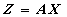
其中,
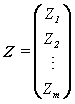 ,
,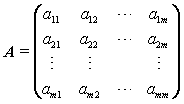 ,
,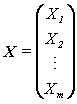
从理论上讲,主成分的个数最多有m个,此时这m个主成分就反映了全部原始变量所提供的信息。鉴于主成分分析的目的是要用少数综合指标来反映全部原始指标中的主要信息,因此在实际应用中,所确定的主成分个数总是小于原始指标的个数。
线性变换的几何意义实际上就是旋转坐标轴。下面通过一组模拟的数据来说明主成分的几何意义。假设有两个原始变量X1和X2,它们之间存在很强的正相关关系。如图1所示,两个变量的散点图中的点几乎都集中在45度线上,即数据的变异几乎都体现在这条直线上。
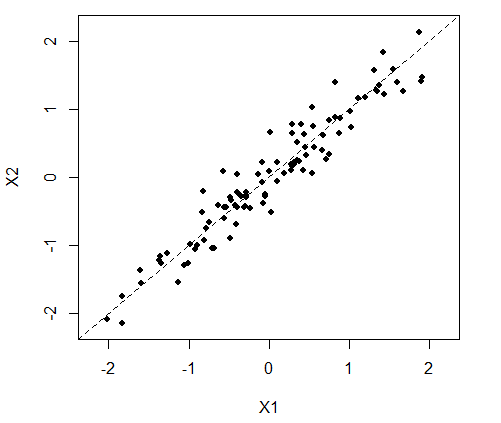
图1原始变量的散点图
如果我们能将两个坐标轴同时逆时针旋转45度,那么只用一个维度(方向)就能够表示数据中绝大多数的变异。图2是旋转坐标轴之后的结果,Z1和Z2分别是X1和X2旋转后的方向,其中Z1就是图1中的45度线,Z2垂直于Z1。从图中我们可以看到数据的变异几乎都体现在了Z1方向上。这样,我们就成功地将二维数据降成了一维数据,而只损失了数据的很小一部分变异。此例只是为了解释主成分分析的原理,并没有太大的实际意义,实际中只有数据中存在多个相关变量时才需要用到主成分分析。
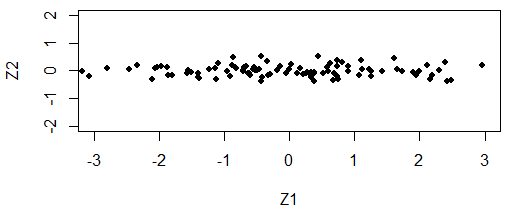
图2旋转坐标轴之后的散点图
求主成分的问题,实际上就是对X的协方差矩阵(或相关系数矩阵)进行特征分解,即求其特征值和特征向量。特征值代表了特征的重要程度,特征向量代表了坐标旋转后的特征方向。base包里的函数eigen( )可以用来求解矩阵的特征值和特征向量。
(三)主成分的求法——手工计算(20分钟)
数据集Harman23.cor是305个女生的八项身体测量指标之间的相关系数,八项指标分别为height(身高)、arm.span(臂展)、forearm(小臂长)、lower.leg(小腿长)、weight(体重)、bitro.diameter(股骨转子间径)、chest.girth(胸围)和chest.width(胸宽)。下面通过对该相关系数矩阵进行特征分解得到主成分。
> cor.matrix <- Harman23.cor$cov
> eigen(cor.matrix)
eigen() decomposition
$values
[1] 4.67287960 1.77098284 0.48103549 0.42144078 0.23322126 0.18667352
[7] 0.13730387 0.09646264
$vectors
[,1] [,2] [,3] [,4] [,5]
[1,] -0.3975776 -0.2797405 -0.10138153 0.10746039 0.4083654
[2,] -0.3893198 -0.3314202 0.11314530 -0.06809937 -0.3409230
[3,] -0.3761601 -0.3446045 0.01526320 0.04696228 -0.5411895
[4,] -0.3883899 -0.2970667 -0.14497535 -0.12381232 0.4586355
[5,] -0.3506669 0.3942422 -0.21329349 0.11448967 0.2957297
[6,] -0.3119078 0.4007179 -0.07323449 0.71279966 -0.2194829
[7,] -0.2855270 0.4359188 -0.42088118 -0.62953051 -0.2571693
[8,] -0.3102250 0.3144488 0.85303619 -0.22086171 0.1095985
[,6] [,7] [,8]
[1,] -0.15193375 0.63598252 -0.384098117
[2,] -0.07209702 0.27848831 0.722612711
[3,] 0.39235508 -0.24188344 -0.481639638
[4,] -0.25086379 -0.66234538 0.112146116
[5,] 0.72009856 0.02630746 0.237305222
[6,] -0.40979597 -0.11197746 -0.006899864
[7,] -0.25828437 0.08024390 -0.125353965
[8,] -0.04071268 -0.03303594 -0.116923142
对相关系数矩阵进行特征分解后得到了从大到小排列的特征值及其对应的单位特征向量。我们先利用特征值决定保留主成分的个数k。一般来说,主成分个数的选取遵循下面两个原则:(1)前k个主成分的累计贡献率达到某一特定的值(比如70%或80%);(2)保留的主成分对应的特征值大于1(Kaiser-Harris准则)。在实际问题中,除了考虑这两个原则,还要结合问题的背景和主成分的实际意义。
> eigen(cor.matrix)$values
[1] 4.67287960 1.77098284 0.48103549 0.42144078 0.23322126 0.18667352
[7] 0.13730387 0.09646264
结果表明,前两个特征值大于1,且前两个特征值之和占特征值总和(总和为变量的个数8)的80.5%,所以可以保留前两个主成分。接下来,由特征值对应的单位特征向量得到各个主成分(为了便于查看,将其保留三位小数)。
> round(eigen(cor.matrix)$vectors, 3)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] -0.398 -0.280 -0.101 0.107 0.408 -0.152 0.636 -0.384
[2,] -0.389 -0.331 0.113 -0.068 -0.341 -0.072 0.278 0.723
[3,] -0.376 -0.345 0.015 0.047 -0.541 0.392 -0.242 -0.482
[4,] -0.388 -0.297 -0.145 -0.124 0.459 -0.251 -0.662 0.112
[5,] -0.351 0.394 -0.213 0.114 0.296 0.720 0.026 0.237
[6,] -0.312 0.401 -0.073 0.713 -0.219 -0.410 -0.112 -0.007
[7,] -0.286 0.436 -0.421 -0.630 -0.257 -0.258 0.080 -0.125
[8,] -0.310 0.314 0.853 -0.221 0.110 -0.041 -0.033 -0.117
上面结果中的各列分别为8个主成分的系数,前两个主成分可表示为:
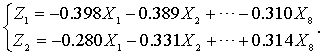
第一个主成分与每个身体测量指标都负相关,且相关系数都比较接近,可以看作一个综合指标;第二个主成分与前四个变量(height、arm.span、forearm和lower.leg)负相关,与后四个变量(weight、bitro.diameter、chest.girth和chest.width)正相关,可以看作一个体型指标。
(四)主成分分析的求法——函数计算(10分钟)
用stats包里的函数princomp( )可以轻松实现主成分分析。需要说明的是,用函数princomp( )做主成分分析可以使用原始数据或者原始数据的协方差矩阵(或相关系数矩阵)。用户可以通过设置其中的参数输入恰当的数据类型,参数的使用方法请查看该函数的帮助文档。本例中只有相关系数矩阵,所以需要将参数covmat设为相关系数矩阵进行主成分分析。
> PCA <- princomp(covmat = cor.matrix)
> summary(PCA, loadings = TRUE)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
Standard deviation 2.1616844 1.3307828 0.69356722 0.6491847 0.48292987
Proportion of Variance 0.5841099 0.2213729 0.06012944 0.0526801 0.02915266
Cumulative Proportion 0.5841099 0.8054828 0.86561224 0.9182923 0.94744500
Comp.6 Comp.7 Comp.8
Standard deviation 0.43205731 0.37054537 0.31058435
Proportion of Variance 0.02333419 0.01716298 0.01205783
Cumulative Proportion 0.97077919 0.98794217 1.00000000
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7 Comp.8
height 0.398 0.280 0.101 0.107 0.408 0.152 0.636 0.384
arm.span 0.389 0.331 -0.113 -0.341 0.278 -0.723
forearm 0.376 0.345 -0.541 -0.392 -0.242 0.482
lower.leg 0.388 0.297 0.145 -0.124 0.459 0.251 -0.662 -0.112
weight 0.351 -0.394 0.213 0.114 0.296 -0.720 -0.237
bitro.diameter 0.312 -0.401 0.713 -0.219 0.410 -0.112
chest.girth 0.286 -0.436 0.421 -0.630 -0.257 0.258 0.125
chest.width 0.310 -0.314 -0.853 -0.221 0.110 0.117
上面把函数princomp( )生成的对象命名为PCA,然后用函数summary( )显示了PCA中的主要信息,其中参数loading默认为FALSE,这里设为TRUE以显示载荷矩阵。在载荷矩阵中,数值的绝对值小于0.1的没有显示,如果想全部显示,可以将参数cutoff设为0。
在选择所需主成分的个数时,我们还可以借助将各主成分的方差排序后的点线图来帮助判断。
> screeplot{XE"screeplot"}(PCA, type = "lines")
> abline(h = 1)
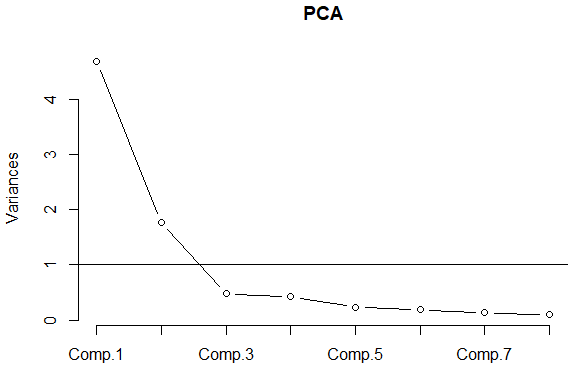
图3数据Harman23.cor的主成分分析碎石图
图3被称为碎石图(scree plot)。“scree”一词来自地质学,表示在岩层斜坡下方发现的小碎石,这些小碎石的地质学价值不高,可以忽略。本例中可见前两个主成分的散点位于陡坡上,而后六个主成分的散点形成了平台,且特征值均小于1,因此保留前两个主成分。
为了分析主成分的意义,我们还可以用函数loadings( )提取载荷矩阵,并用其前两列作散点图(如图4),代码如下:
> load <- loadings(PCA)
> plot(load[, 1:2], xlim = c(-0.5, 0.5), ylim = c(-0.5, 0.5))
> text(load[, 1], load[, 2], adj = c(-0.3, 0))
> abline(h = 0, v = 0)
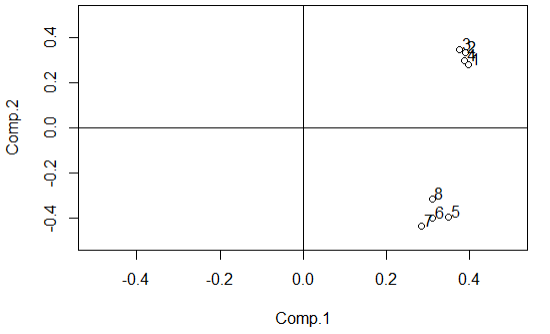
图4数据Harman23.cor的8个变量在前两个主成分下的散点图
